物理竞赛

前言

之前看到了Jesse Berezovsky的工作[1]就想出一道题，奈何一些计算如果只用计算器还是不太够只能放弃了。但是这个问题还是很有意思的，所以就写一下。

音乐具有复杂的旋律，但是又追求协和的声乐效果。联想到一些特殊的热学量，我们可以用内能UU来表示“不协和程度”，熵SS表示“复杂度”，那么一个“音乐系统”的自由能就是F=U−TSF=U-TS，而最自然的系统应当最小化自由能。

简化起见，我们假定乐器的声音是锯齿波，频率为ff的锯齿波y(t)=fAt (0≤ft≤0.5)y(t)=fAt\ (0≤ft≤0.5)的傅里叶级数如下

\begin{align} y(t) = \frac{A}{2} - \frac{A}{\pi}\sum_{j=1}^\infty\frac{\sin2\pi fjt}{j} \end{align}

相互作用能与音律

热力学系统

内能既然代表不协和程度，而不协和一定是对多个音调之间关系的描述，也即所谓的“相互作用能”。我们首先只考虑两个音调的情况，即faf_a和fbf_b。根据上面的傅里叶级数，在频域上对应着{fa,2fa,⋯ ,nfa,fb,2fb,⋯ ,nfb}\{f_a,2f_a,\cdots,nf_a,f_b,2f_b,\cdots,nf_b\}几个频率，我们将之视作一个有2n2n个粒子的一维热力学系统。

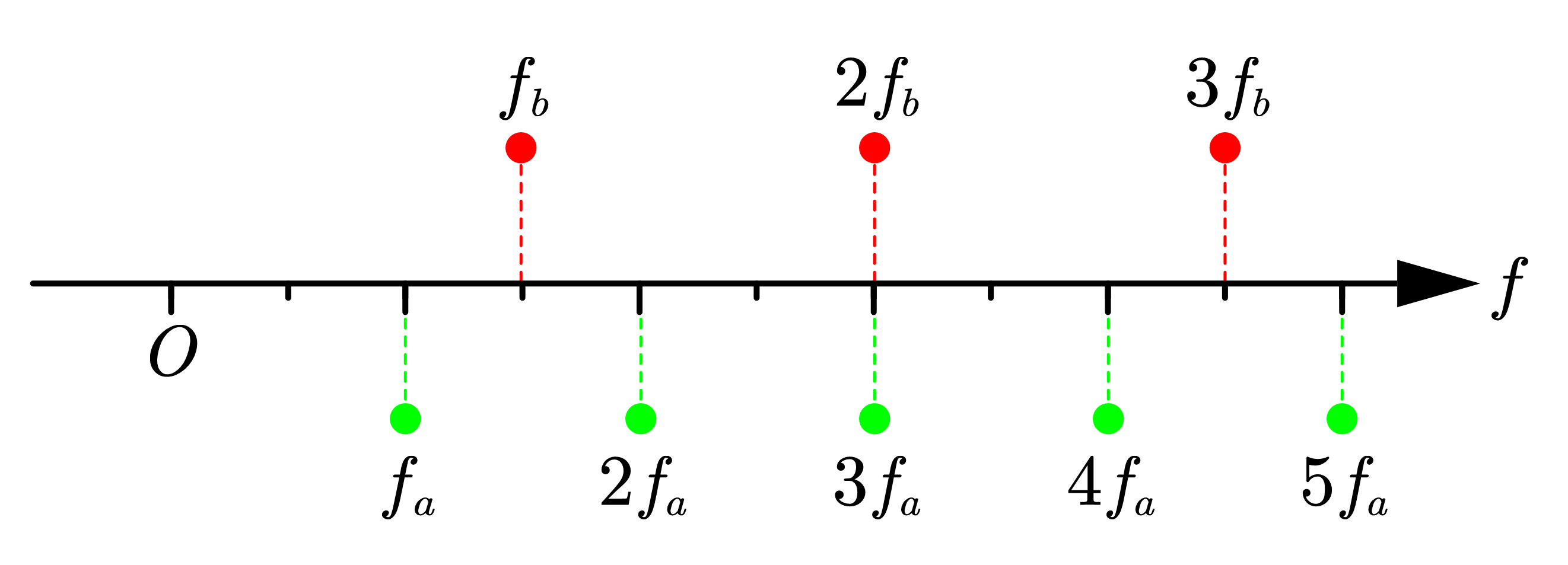图1: 两个音调对应的热力学系统

在这里为了后续的计算方便对频率进行了截断处理，但是这并不影响结论的正确性。而且人耳受到高频影响较小，所以这个截断是合理的。

两个频率的不和谐度

Bernini和Talamucci[2]通过声学实验为我们定量化了人耳对两个频率的不和谐度的感知。因此我们基于其实验结论可以得到计算两个频率fa,fb (fa<fb)f_a,f_b\ (f_a<f_b)的不和谐度的经验公式，即相互作用能

\begin{align} u_{ab}=\begin{cases} \frac{6.1\Delta}{\delta}e^{1-\frac{6.1\Delta}{\delta}}, & f_b\leq1.2f_a \\ 0, & f_b>1.2f_a \end{cases} \end{align}

其中Δ=fb−fa\Delta=f_b-f_a为频率差，δ\delta则被称作临界带宽（critical bandwidth），其计算经验公式如下

\begin{align} \delta=1.065\times10^{-5}\bar{f}^2+0.1145\bar{f}+50.3559\ (\text{Hz}) \end{align}

❗请注意上述公式由笔者为方便计算而简化的拟合公式得到，因此计算结果也与原文有些许不同，准确的实验结果以及经验公式请参考原文[2]。

相互作用能与音律的来源

我们可以将两个频率的相互作用能视作一个“键”（bond），而系统的内能就是所有键的总和。这样我们就可以得到系统的相互作用能为

\begin{align} U_{ab}=\sum_{i=1}^{n}\sum_{j=i+1}^{n}u_{ij} \end{align}

以中央C音fC=261.626 Hzf_C=261.626\ \text{Hz}为基准作为例子，我们计算一个八度内其他音调与中央C音的不和谐度。计算代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
import numpy as np
import matplotlib.pyplot as plt

# 临界宽带
def critical_bandwidth(freq):
    delta = 1.065e-5 * freq**2 + 0.1145 * freq + 50.3559
    return delta

# 两频率间的不和谐度
def dissonance(f1, f2):
    fmin = min(f1, f2)
    fmax = max(f1, f2)
    if fmax > 1.2 * fmin:
        return 0
    delta_f = fmax - fmin
    delta = critical_bandwidth((f1 + f2) / 2)
    tmp = 6.1 * delta_f / delta
    return tmp * np.exp(1 - tmp)

# 两音调总不和谐度
def dissonance_total(f1, f2, n):
    dissonance_sum = 0
    for i in range(1, n):
        for j in range(1, n):
            dissonance_sum += dissonance(f1 * i, f2 * j)
    return dissonance_sum

# 绘制不和谐度图
def plot_dissonance(f, n):
    x = np.linspace(1, 2, 5000)
    y = np.zeros(5000)
    for i in range(5000):
        y[i] = dissonance_total(f, f * x[i], n)
    plt.plot(x, y)
    plt.xlabel('Frequency Ratio')
    plt.ylabel('Dissonance')
    plt.title('Dissonance of Two Tones')
    plt.show()

# 主函数
if __name__ == '__main__':
    f = 261.626
    n = 8
    plot_dissonance(f, n)

计算结果如下图所示，可以发现其中存在一些极小值点，而计算这些点的位置我们会发现这些点正好对应着1:11:1,1:21:2（齐音和八度）,2:32:3（五度）,3:53:5（大六度）,3:43:4（四度）,5:65:6（小三度）,4:54:5（大三度），这些音程正是音乐中常见的音程。

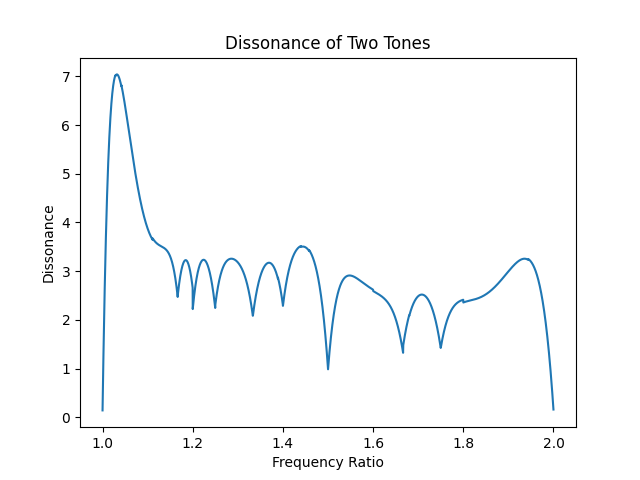图2: 以中央C音为基准的不和谐度结果

最自然的系统

概率函数与热力学量

如果已知前一个音， 那么下一个音有可能是什么？对于下一个音的概率的描述，即可视作我们对于音乐系统热力学分布的描述。考虑到一个八度相差的两个音具有相似性，我们只考虑八度内的范围。假设基准音高为f0f_0，记f=f0⋅2x (0≤x≤1)f=f_0\cdot2^x\ (0\leq x\leq1)，那么其概率函数为p(x)p(x)。

热力学量便可借由概率函数表达，首先是熵。我们借用香农关于信息熵的定义，因此可以得到系统的熵为

\begin{align} S=-\int_{0}^{1}p(x)\ln p(x)\text{d}x \end{align}

内能我们首先定义一个相互作用能的平均值，即U‾(x)=∑n=−∞+∞U(f0,f0⋅2x+n)\overline{U}(x)=\sum_{n=-\infty}^{+\infty}U(f_0,f_0\cdot2^{x+n})，那么系统的内能为

\begin{align} U=\frac{1}{2}\int_{0}^{1}\int_{0}^{1}p(x)\overline{U}(x-y)p(y)\text{d}x\text{d}y \end{align}

最后该问题事实上成为了在不同TT下求解p(x)p(x)以最小化系统的自由能F=U−TSF=U-TS，注意p(x)p(x)满足归一化约束∫01p(x)dx=1\int_{0}^{1}p(x)\text{d}x=1。

变分法求解

由于最自然的系统使得FF有极小值，因此我们可以通过变分法求解。首先我们可以得到自由能的变分

δF=∫01[∫01U‾(x−y)p(y)dy+T(1+ln⁡p(x))]δp(x)dx=∫01[∫01U‾(x−y)p(y)dy+Tln⁡p(x)]δp(x)dx\begin{aligned} \delta F&=\int_{0}^{1}\left[\int_{0}^{1}\overline{U}(x-y)p(y)\text{d}y+T(1+\ln p(x))\right]\delta p(x)\text{d}x\\ &=\int_{0}^{1}\left[\int_{0}^{1}\overline{U}(x-y)p(y)\text{d}y+T\ln p(x)\right]\delta p(x)\text{d}x \end{aligned}

上式利用到了约束条件的变分∫01δp(x)dx=0\int_{0}^{1}\delta p(x)\text{d}x=0。根据极值条件δF=0\delta F=0，可以得到p(x)p(x)满足的积分方程

\begin{align} &\int_{0}^{1}\overline{U}(x-y)p(y)\text{d}y+T\ln p(x)=\text{const}\\ \implies &p(x)=\frac{\exp\left[-\frac{1}{T}\int_{0}^{1}\overline{U}(x-y)p(y)\text{d}y\right]}{\int_{0}^{1}\exp\left[-\frac{1}{T}\int_{0}^{1}\overline{U}(z-y)p(y)\text{d}y\right]\text{d}z} \end{align}

该方程可以通过迭代法求解，将方程视作p(x)=Q^p(x)p(x)=\hat{Q}p(x)，其中Q^\hat{Q}为一个算符，那么我们可以通过迭代p(x)=Q^np(x)p(x)=\hat{Q}^np(x)来求解。为了减少震荡，可以引入一个松弛参数α\alpha，有p(x)=αp(x)+(1−α)Q^p(x)=Qˉp(x)p(x)=\alpha p(x)+(1-\alpha)\hat{Q}p(x)=\bar{Q}p(x)，其中Qˉ=αI+(1−α)Q^\bar{Q}=\alpha I+(1-\alpha)\hat{Q}。

计算代码如下（此处取中央C音为基准进行了计算）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
import numpy as np
import matplotlib.pyplot as plt

# 略去不和谐度计算的实现

# 核函数U
def U(f, x):
    res = 0
    for i in range(-5, 5):
        res += dissonance_total(f, f * np.float_power(2, x + i), 8) 
    return res

# 预处理U函数
def Upre(f):
    x = np.linspace(0, 2, 2000)
    y = np.zeros(2000)
    for i in range(2000):
        y[i] = U(f, x[i] - 1)
    return y

# 预处理积分函数
def prefun(p, T, f, U1):
    y = np.zeros(1000)
    for i in range(1000):
        for j in range(1000):
            y[i] += U1[1000+i-j] * p[j] * 0.001
        y[i] = np.exp(-(y[i] / T))
    return y

# Q算符
def Q(p, T, f, U1):
    ans = prefun(p, T, f, U1)
    intans = np.sum(ans) * 0.001
    y = ans / intans
    return y

# 绘制p(x)
def plot_p(p, label):
    x = np.linspace(0, 1, 1000)
    plt.plot(x, p, label=label)

#主函数
if __name__ == '__main__':
    f = 261.626
    T_values = [0.3, 0.6, 10]
    a = 1 / 3
    U1 = Upre(f)

    for T in T_values:
        p = np.ones(1000) / 1000
        for i in range(50):
            q = Q(p, T, f, U1)
            p = a * p + (1 - a) * q
        plot_p(p, label=f'T={T}')

    plt.xlabel('x')
    plt.ylabel('p(x)')
    plt.ylim(0, 1.2)
    plt.title('p(x) for different T values')
    plt.legend()
    plt.show()

计算结果如下图所示，可以发现p(x)p(x)在不同的TT下明显有着不同的分布。

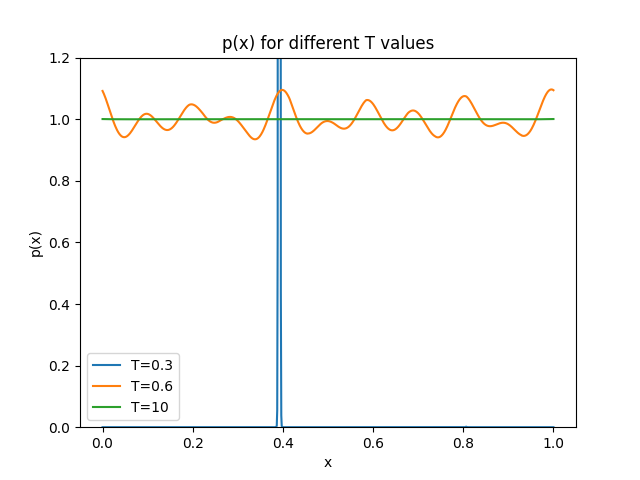图3: 不同温度下的概率分布

相变

系统的相

如果TT极小，意味着系统并不追求复杂性的变化，那么p(x)p(x)会更加集中在某些音调上；而如果TT极大，系统会追求更多的变化，因此p(x)p(x)在不同音调上的概率会更加平均；而TT还存在一个区间，使得p(x)p(x)有着波动状的分布。

既然我们已经发现了p(x)p(x)在不同TT下的分布存在明显的差异，一个很自然的想法就是系统存在着相变，而该系统存在着三个相，按照温度TT从高到低依次记为Ⅰ，Ⅱ，Ⅲ相。相变温度记为Tc1,Tc2 (Tc1>Tc2)T_{c1}, T_{c2}\ (T_{c1}>T _{c2})。

二级相变

系统从Ⅰ相到Ⅱ相的相变是一个二级相变，这是因为系统的熵在相变点处不连续。我们使用朗道理论来描述这个相变，首先进行傅里叶展开U‾(x)=∑k=0+∞ukcos⁡2πkx,p(x)=12∑k=0+∞(pke2πikx+pk∗e−2πikx)\overline{U}(x)=\sum_{k=0}^{+\infty}u_k\cos2\pi kx, p(x)=\frac{1}{2}\sum_{k=0}^{+\infty}\left(p_ke^{2\pi ikx}+p_k^*e^{-2\pi ikx}\right)，并代入计算得到

\begin{align} U=\frac{1}{2}u_0+\frac{1}{8}\sum_{k=1}^{+\infty}d_k|p_k|^2 \end{align}

\begin{align} S=\sum_{n=2}^{+\infty}\frac{(-1)^{n-1}}{n(n-1)2^n}\int_0^1\left(\sum_{k=0}^{+\infty}\left(p_ke^{2\pi ikx}+p_k^*e^{-2\pi ikx}\right)\right)^n\text{d}x \end{align}

在Tc1T_{c1}附近展开，我们可以得到

\begin{align} F\approx\frac{1}{2}u_0+\frac{1}{4}\sum_{k=1}^{+\infty}\left(\frac{u_k}{2}+T\right)|p_k|^2 \end{align}

假设最高阶项为正值，当二阶项的符号发生变化时，就会发生相变。因此，当TT从无序阶段减小时，具有最大负值uk=uk0u_k=u_{k_0}的项将首先改变符号，单模 k0k_0将具有非零的pk0p_{k_0}，因此根据朗道理论我们可以得到

\begin{align} T_{c1}=-\frac{u_{k_0}}{2} \end{align}

一级相变

系统从Ⅱ相到Ⅲ相的相变是一个一级相变，这是因为系统的熵在相变点处连续。但是内能在相变点处会发生突变。在此采用简单的半定量说明内能突变大小。

在Ⅲ相其近似为集中在一个音调上，因此我们取p(x)=δ(x−x0)p(x)=\delta(x-x_0)，那么系统的内能为

\begin{align} U=\frac{1}{2}\overline{U}(0) \end{align}

而在刚刚过渡至Ⅱ相，我们取p(x)=(1−λ)δ(x−x0)+λδ(x−x1)p(x)=(1-\lambda)\delta(x-x_0)+\lambda\delta(x-x_1)，也即另一个音调略微出现，那么系统的内能为

\begin{align} U=\frac{1}{2}\overline{U}(0)+\lambda(1-\lambda)\left(\overline{U}(x_1-x_0)-\overline{U}(0)\right) \end{align}

结语

Jesse Berzovsky的工作[1]在后续还提供了更为完整和复杂的对整首乐曲的分析，并且类比XY模型，提出了音乐的“相变”概念。建议阅读原文以获得更多信息。

  1. 1.Jesse Berezovsky, The structure of musical harmony as an ordered phase of sound: A statistical mechanics approach to music theory. Sci. Adv. 5, eaav8490(2019).DOI:10.1126/sciadv.aav8490 ↩
  2. 2.Bernini, A. and Talamucci, F. (2014) Consonance of Complex Tones with Harmonics of Different Intensity. Open Journal of Acoustics, 4, 78-89. doi: 10.4236/oja.2014.42008. ↩